Tesszaláció

Ez a szócikk vagy szakasz lektorálásra, tartalmi javításokra szorul. A felmerült kifogásokat a szócikk vitalapja részletezi (vagy extrém esetben a szócikk szövegében elhelyezett, kikommentelt szövegrészek). Ha nincs indoklás a vitalapon (vagy szerkesztési módban a szövegközben), bátran távolítsd el a sablont! Csak akkor tedd a lap tetejére ezt a sablont, ha az egész cikk megszövegezése hibás. Ha nem, az adott szakaszba tedd, így segítve a lektorok munkáját!

A tesszaláció az a folyamat, amikor egy kétdimenziós síkon egy geometriai formát ismételnek átfedés és rések nélkül. A folyamatot magasabb dimenziókra is ki lehet terjeszteni (pl. tér hézagmentes kitöltése). A tesszaláció megfigyelhető az ókori építészettől a modern művészetekig és a természetben is. Egy építészeti példa a granadai Alhambra tetőcserepei, mely a neves művészt, M. C. Eschert is inspirálta. A természetben a méhsejt felépítése is tesszaláció.

1618-ban Johannes Kepler dokumentálta először a tesszalációt. 1891-ben Jevgraf Fjodorov orosz krisztallográfus megfigyelései indították el a tesszaláció matematikai tanulmányozását. A számítógépes grafika gyakran használja a tesszalációs technikát téglalap alakú szerkezetek összeállítására. 3D testek analízise gyakran elég komplikált feladat. Ezért tesszalációs módszerekkel, kis hálózatokra való bontással közelítik. Ez a módszer felhasználható a végeselemes módszer alkalmazására is. Geodézikus kupoláknál is gyakran használják a tesszalációt. Erre példa a Walt Disney Világban a Föld-űrhajó-modell.

A transzlációs szimmetriákat a tapétacsoportokkal kategorizálják, melyekből 17-et tartanak nyilván.^[1] Mind a 17 csoporttag látható a Alhambra-palotában (Granada, Spanyolország). A tesszalációs mintákra is érvényes a négyszín-tétel. A tétel szerint minden mintát ki lehet úgy színezni legfeljebb négy szín felhasználásával, hogy ne legyen két azonos színű szomszédos terület.

A szabályos tesszalációk teljesen szimmetrikusak, melyek egybevágó sokszögekből épülnek fel. Csupán háromféle szabályos tesszaláció létezik: egyenlő oldalú háromszögek, négyzetek és szabályos hatszögek.^[2] A félig szabályos tesszalációk a szabályos sokszögek variációit használják. Más tesszalációk is ismertek, mint szabályos–nem szabályos, szimmetrikus–aszimmetrikus, fraktál- és egyéb változtatok.

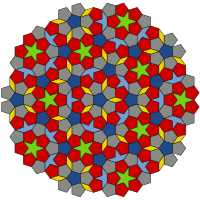
A leghíresebb aperiodikus tesszaláció, a Penrose-féle csempézés két különböző sokszöget használ. A Penrose-féle csempézés az aperiodikus mintaosztályhoz tartozik, mely önismétléssel képződik, rekurziót használva.

A monohedrális mintázat^[3] jellemzője, hogy minden minta egybevágó. Létezik spirális monohedrális mintázat, melynek alapeleme egy nemkonvex kilencszög.

Vegyes mintára példa a marrákesi mintázat.

Tesszaláció elvégezhető tórusz és gömb felületén is.

• Bazaltmintázat Észak-Írországban.
• Tasmaniában látható egy üledékes sziklákból kialakult tesszalációs minta, mely úgy néz ki, mintha emberek alkották volna.
• A botanikában számos példa található a tesszalációra: virágok, gyümölcsök, levelek stb. Az őszi kikerics ennek egyik szép példája.

• http://mathworld.wolfram.com/RegularTessellation.html
• http://www.nomadinception.com/gallery-arabic-patterns-islamic-patterns-research.aspx
• http://msdn.microsoft.com/en-us/library/ff476340%28v=VS.85%29.aspx