Euklideszi tér (lineáris algebra)

A „Tér” lehetséges további jelentéseiről lásd: Tér (egyértelműsítő lap).

Euklideszi térnek^{[* 1]} nevezzük azon véges dimenziós valós vektortereket, melyekben a vektorterek axiómáin felül értelmezve van egy skaláris szorzat. A skaláris szorzat alapján definiálható egy vektor hossza, illetve két vektor hajlásszöge, így az euklideszi terekben lehet geometriát végezni. Az euklideszi vektorterek közvetlen általánosításai a skalárszorzatos vektorterek.

Legyen V egy véges dimenziós valós vektortér. A ${\displaystyle \langle -,-\rangle :V\times V\to \mathbb {R} }$ leképezést skalárszorzatnak nevezzük, ha teljesíti a következő feltételeket:

1. Pozitív definit: bármely két ${\displaystyle u,v\in V}$ vektorra ${\displaystyle \langle u,v\rangle \geq 0}$, továbbá ${\displaystyle \langle u,u\rangle =0}$ pontosan akkor, ha ${\displaystyle u=0}$.
2. Szimmetrikus: bármely két ${\displaystyle u,v\in V}$ vektorra ${\displaystyle \langle u,v\rangle =\langle v,u\rangle }$.
3. Bilineáris, azaz mindkét változójában lineáris: bármely ${\displaystyle u,v,w\in V}$ vektorra és ${\displaystyle \lambda \in \mathbb {R} }$ skalárra

   ${\displaystyle \langle u+\lambda w,v\rangle =\langle u,v\rangle +\lambda \langle w,v\rangle }$ és ${\displaystyle \langle u,v+\lambda w\rangle =\langle u,v\rangle +\lambda \langle u,w\rangle }$.

A skalárszorzatot nevezik még belső szorzatnak is. Két vektor skaláris szorzatának jelölésére ${\displaystyle \langle u,v\rangle }$ mellett az ${\displaystyle u\cdot v}$ illetve az ${\displaystyle uv}$ képlet is használatos. Egy skalárszorzattal ellátott véges dimenziós vektorteret euklideszi térnek nevezünk.

Legyen ${\displaystyle e_{1},e_{2},\ldots ,e_{n}}$ egy bázis V-ben. Ekkor az ehhez a bázishoz tartozó skaláris szorzatot a következő képlet definiálja:

${\displaystyle \left\langle \sum _{i=1}^{n}x_{i}e_{i},\sum _{i=1}^{n}y_{i}e_{i}\right\rangle =\sum _{i=1}^{n}x_{i}y_{i}}$.

Könnyen látható, hogy az így definiált leképezés pozitív definit, szimmetrikus és bilineáris, azaz megfelel a fenti definíciónak. A szakirodalom egy része csak ezt a bázishoz tartozó skaláris szorzatot taglalja.

Ha ${\displaystyle (V,\langle -,-\rangle )}$ egy euklideszi tér és ${\displaystyle U\leq V}$ egy altér, akkor a skalárszorzat U-ra történő megszorításával U is euklideszi tér.

A skalárszorzat kielégíti a Cauchy–Bunyakovszkij–Schwarz-egyenlőtlenséget: ha ${\displaystyle u,v\in V}$, akkor ${\displaystyle \langle u,v\rangle ^{2}\leq \langle u,u\rangle \cdot \langle v,v\rangle }$.

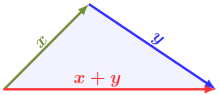
Egy ${\displaystyle (V,\langle -,-\rangle )}$ euklideszi térben egy v vektor hosszát a

${\displaystyle \|v\|={\sqrt {\langle v,v\rangle }}}$

képlet definiálja. A skalárszorzat pozitív definit volta miatt a négyzetgyök alatt mindig egy nemnegatív szám áll, így a fenti képlet értelmes. A Cauchy–Bunyakovszkij–Schwarz-egyenlőtlenségből következik, hogy ez a hosszfogalom kielégíti a háromszög-egyenlőtlenséget, azaz bármely ${\displaystyle u,v\in V}$ vektorokra

${\displaystyle \|u+v\|\leq \|u\|+\|v\|}$.

Ha ${\displaystyle u,v\in V}$ vektorok, akkor az általuk bezárt ${\displaystyle \varphi }$ szöget a következő képlet definiálja:

${\displaystyle \cos \varphi ={\frac {\langle u,v\rangle }{\|u\|\cdot \|v\|}}}$.

A jobb oldal a Cauchy–Bunyakovszkij–Schwarz-egyenlőtlenség szerint pozitív, így valóban létezik olyan szög, aminek ez a koszinusza. Ez a definíció a koszinusztétel általánosítása. Egy euklideszi vektortérben két vektort ortogonálisnak vagy merőlegesnek nevezünk, ha az általuk bezárt szög derékszög; ezzel ekvivalens, hogy a két vektor skalárszorzata nulla.

Egy bázist ortogonálisnak nevezünk, ha az azt alkotó vektorok páronként ortogonálisak egymásra. A bázis ortonormált, ha ortogonális és minden bázisvektor egység hosszú. Bármely ortogonális bázis ortonormálttá alakítható az egyes bázisvektorok normálásával, azaz úgy, hogy minden egyes vektort elosztunk a saját hosszával. Általánosabban, egy tetszőleges bázis ortonormálttá alakítható a Gram–Schmidt-eljárással.

• Freud Róbert. Lineáris algebra, javított és bővített kilencedik kiadás (magyar nyelven) (2024). ISBN 9634630804 
• Gerd Fischer. Lineare Algebra – Eine Einführung für Studienanfänger, tizenkilencedik kiadás (német nyelven), Springer (2020). ISBN 978-3-662-61645-1