Hipergráf
A mai világban a Hipergráf olyan téma, amely nagy jelentőségűvé vált, és jelentős hatást gyakorolt a társadalomra. Az idő múlásával a Hipergráf egyre fontosabbá vált különböző területeken, vitákat, vitákat és elemzéseket generálva relevanciájával és következményeivel kapcsolatban. Ezért elengedhetetlen, hogy elmélyüljünk a Hipergráf tanulmányozásában és megértésében, mivel megértése és elemzése transzcendentális ahhoz, hogy megértsük azt a világot, amelyben élünk. Ebben a cikkben a Hipergráf-hez kapcsolódó különböző dimenziókba és szempontokba fogunk beleásni, azzal a céllal, hogy átfogó képet adjunk erről a témáról és a mai társadalomra gyakorolt hatásairól.
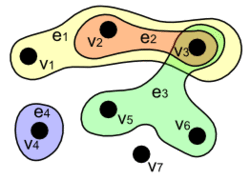
A hipergráf vagy halmazrendszer a kombinatorika által vizsgált matematikai struktúrák egyike; elméletük a gráfelméletből vált le; mert a gráfok olyan általánosításainak tekinthetőek, ahol egy él kettőnél több csúcsot is összeköthet („hiperélek”). Az elnevezés bevezetésére Claude Berge francia kombinatorikaprofesszor tett javaslatot 1966-ban egy tihanyi matematikustalálkozón, és ő írta a hipergráfok elméletének első összefoglaló munkáit is.
Matematikailag egy hipergráf egy (V,E) páros, ahol V tetszőleges (általában, de nem szükségszerűen: véges) halmaz, E pedig a V részhalmazainak egy családja; bár ha pontosak akarnánk lenni, azt mondanánk, hogy egy hipergráf valójában ilyen párok egy ekvivalenciaosztálya az izomorfia nevű relációra nézve. A V elemeit (hiper)csúcsoknak, az E elemeit (hiper)éleknek is szokás nevezni.
A hipergráfok tulajdonképpen az incidenciastruktúrák közé tartoznak. Megfordítva, az incidenciastruktúrák is tekinthetők hipergráfoknak. Például minden hipergráfnak megvan az illeszkedési gráfja, és megfordítva. Hipergráf helyett használják a halmazrendszer és a halmazcsalád elnevezéseket is.
Az egyszerű hipergráf (az egyszerű gráf mintájára) olyan hipergráf, melyben egyik hiperél sem tartalmazza a másikat (két csúcsot legfeljebb egy hiperél köt össze).
Egy n-uniform hipergráf alatt olyan hipergráfot értünk, ahol minden hiperél n csúcsot köt össze. Így a sima gráfok voltaképpen 2-uniform hipergráfok.
Külső hivatkozások
- Planetmath.org oldala a hipergráfokról.
- R. L. Graham - M. Grötschel - Lovász L.: Handbook of combinatorics. MIT Press, 1995. ; 7. fejezet.
- Weisstein, Eric W.: Hipergráf (angol nyelven). Wolfram MathWorld
|
Ez a matematikai tárgyú lap egyelőre csonk (erősen hiányos). Segíts te is, hogy igazi szócikk lehessen belőle! |